Радуга

Радуга
Как средь прозрачных облачных пелен
Над луком лук соцветный и сокружный
Посланницей Юноны вознесен,
И образован внутренним наружный.
Данте


Радуга у всех на виду - она обычно наблюдается в виде двух окрашенных дуг (двух соцветных луков, о которых пишет Данте), причем в верхней дуге цвета располагаются в таком порядке сверху вниз: фиолетовый, синий, голубой, зеленый, желтый, оранжевый, красный, а в нижней дуге наоборот - от красного до фиолетового. Для запоминания их последовательности есть мнемонические фразы, первые буквы каждого слова в которых соответствуют первым буквам названия цвета Например, такой является фраза "Каждый Охотник Желает Знать, Где Сидит Фазан" или другая, не менее известная, "Как Однажды Жан-Звонарь Головою Сшиб Фонарь". Правда, традиция выделять в радуге 7 цветов не всемирна. Например, у болгар в радуге 6 цветов.

Радуга даёт уникальную возможность наблюдать в естественных условиях разложение белого света в спектр.
Радуга обычно появляется после дождя, когда Солнце стоит довольно низко. Где-то между Солнцем и наблюдателем ещё идёт дождь. Солнечный свет, проходя сквозь капли воды, многократно отражается и преломляется в них, как в маленьких призмах, и лучи разного цвета выходят из капель под различными углами. Это явление называется дисперсией (т. е. разложением) света. В результате образуется яркая цветная дуга (а на самом деле крут; целиком его можно увидеть с самолёта).
Иногда наблюдаются сразу две, реже - три разноцветные дуги. Первую радугу создают лучи, отразившиеся внутри капель однократно, вторую - лучи, отразившиеся дважды, и т. д. В 1948 г. в Ленинграде (ныне Санкт-Петербург) среди туч над Невой появилось сразу четыре радуги.


Вид радуги, яркость цветов, ширина полос зависят от размеров и количества водяных капель в воздухе. Яркая радуга бывает летом после грозового дождя, во время которого падают крупные капли. Как правило, такая радуга предвещает хорошую погоду.
В яркую лунную ночь можно увидеть радугу от Луны. Радуга возникает в свете полной луны, когда идет дождь. Поскольку человеческое зрение устроено так, что при слабом освещении наиболее чувствительные рецепторы глаза - "палочки" - не воспринимает цвета, лунная радуга выглядит белесой; чем ярче свет, тем "цветнее" радуга (в её восприятие включаются цветовые рецепторы - "колбочки").

огненная радуга
Ее повезло увидеть жительнице Швеции Мариан Эриксон. Радуга протянулась по ночному небу и стояла при полной луне в течение минуты.
Приметы и легенды.
Когда-то давным-давно человек стал задумываться, почему же на небе появляются радуги. В те времена об оптике даже и не слышали. Потому люди придумывали мифы и легенды, а так же существовало множество примет. Вот некоторые из них:
- В скандинавской мифологии радуга - это мост Биврёст, соединяющий Мидгард (мир людей) и Асгард (мир богов).
- В древнеиндийской мифологии - лук Индры, бога грома и молнии.
- В древнегреческой мифологии - дорога Ириды, посланницы между мирами богов и людей.
- По славянским поверьям, радуга, подобно змею, пьёт воду из озёр, рек и морей, которая потом проливается дождём.
- Ирландский лепрекон прячет горшок золота в месте, где радуга коснулась земли.
- По чувашским поверьям, если пройти сквозь радугу, то можно поменять пол.
- В Библии радуга появилась после всемирного потопа как символ прощения человечества.
- Суеверные люди считали, что радуга является плохим предзнаменованием. Они считали, что души умерших переходят в потусторонний мир по радуге, и если появилась радуга, это означает чью-то близкую кончину.

История объяснения радуги.
Уже Аристотель, древнегреческий философ, пытался объяснить причину радуги. А персидский астроном Qutb al-Din al- Shirazi (1236-1311), а возможно, его ученик Kamal al-din al-Farisi (1260-1320), видимо, был первым, кто дал достаточ но точное объяснение феномена.
Общая физическая картина радуги была уже четко описана Марком Антонием де Доминисом (1611).

М.А. де Доминис
На основании опытных наблюдений он пришел к заключению, что радуга получается в результате отражения от внутренней поверхности капли дождя и двукратного преломления - при входе в каплю и при выходе из нее. Рене Декарт дал более полное объяснение радуги в своем труде "Метеоры" в главе "О радуге" (1635).

Рене Декарт
Декарт пишет:
"Во-первых, когда я принял во внимание, что радуга может появляться не только на небе, но также и в воздухе вблизи нас каждый раз, когда в нем находятся капли воды, освещенные солнцем, как это иногда можно видеть в фонтанах, мне легко было заключить, что она зависит от того, каким образом лучи света действуют на эти капли, а от них достигают нашего глаза; далее, зная, что эти капли шарообразны, и видя, что и при больших и при малых каплях радуга появляется всегда одинаковым образом, я поставил себе целью создать очень большую каплю, чтобы иметь возможность лучше ее рассмотреть. Для этого я наполнил водой большой стеклянный сосуд, вполне круглый и вполне прозрачный и пришел к следующему выводу..."
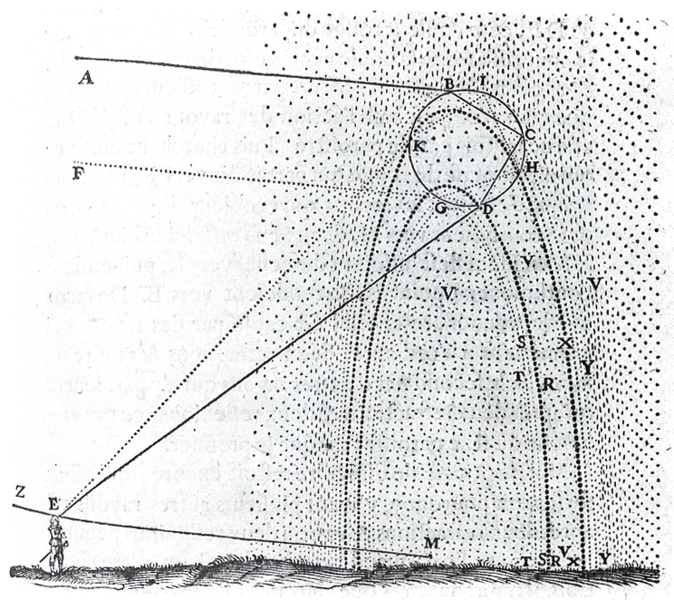
Этот вывод повторяет и уточняет результат, полученный Доминисом. В частности, Декарт обнаружил, что вторая (внешняя) радуга возникает в результате двух преломлений и двух отражений. Он также качественно объяснил появление цветов радуги, сравнивая преломление света в капле с преломлением в стеклянной призме. Рисунок 1, поясняющий ход луч ей в капле, взят из упомянутой выше работы Декарта. Но главная заслуга Декарта заключалась в том, что он колич ественно объяснил это явление, впервые используя закон преломления света:
"Я еще не знал, почему цвета появляются лишь под известными углами, пока не взял перо и не вычислил подробно хода всех лучей, которые падают на различные точ ки водяной капли, чтобы узнать, под какими углами они могут попасть в наш глаз после двух преломлений и одного или двух отражений. Тогда я нашел, что после одного отражения и двух преломлений гораздо больше лучей, которые могут быть видны под углом от 41° до 42° (по отношению к солнечному лучу), чем таких, которые видны под каким-либо меньшим углом, и нет ни одного, который был бы виден под большим. Далее я нашел также, что после двух отражений и двух преломлений оказывается гораздо больше лучей, падающих в глаз под углом от 51° до 52°, чем таких, которые бы падали под каким-либо большим углом, и нет совсем таких, которые падали бы под меньшим".
|
|
|
Рис. 1. Рисунок из работы Р. Декарта, поясняющий наблюдение радуги. |
Таким образом, Декарт не только вычисляет ход лучей, но и определяет угловое распределение интенсивности рассеянного каплями света.
В отношении цветов теория дополнена Исааком Ньютоном.

Исаак Ньютон
Хотя многоцветный спектр радуги непрерывен, по традиции в нем выделяют 7 цветов. Считают, что первым выбрал число 7 Исаак Ньютон, для которого число 7 имело специальное символическое значение (по пифагорейским, богословским или умерологическим соображениям).
В известных "Лекциях по оптике", которые были написаны в 70-х годах XVI века, но опубликованы уже после смерти Ньютона в 1729 году, приведено следующее резюме:
"Из лучей, входящих в шар, некоторые выходят из него после одного отражения, другие - после двух отражений; есть лучи, выходящие после трех отражений и даже большего числа отражений. Поскольку дождевые капли очень малы относительно расстояния до глаза наблюдателя, то не стоит совсем рассматривать их размеры, а только углы, образуемые падающими лучами с выходящими. Там, где эти углы наибольшие или наименьшие, выходящие лучи наиболее сгущены. Так как различные роды лучей (лучи разных цветов) составляют различные наибольшие и наименьшие углы, то лучи, наиболее плотно собирающиеся у различных мест, имеют стремление к проявлению собственных цветов".
Утверждение Ньютона о возможности не учитывать размеры капли, так же как слова Декарта о том, что при больших и малых каплях радуга появляется всегда одинаковым образом, оказалось неточным. Полная теория радуги с учетом дифракции света, которая зависит от соотношения длины волны света и размера капли, была построена лишь в XIX веке Дж.Б. Эри ( 1836) и Дж.М. Пернтером (1897).
Преломление и отражение луча в капле воды.
Рисунок Декарта, который мы воспроизвели как реликвию, обладает одним "методическим" несовершенством. Неподготовленному читателю может показаться, что обе радуги, внешняя и внутренняя, обусловлены разными способами отражения в одной и той же капле. Лучше было бы изобразить две капли: одну, относящуюся к нижней радуге, другую к верхней, оставив в каждой по одному способу отражения, как это показано на рис. 2. Для простоты восприятия в обоих случаях направление падающего на каплю солнечного луча принято за ось абсцисс. Координату y, характеризующую точку падения луча на каплю, будем называть прицельным параметром.
|
|
|
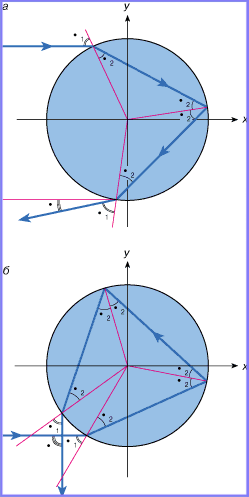
Рис. 2. Ход лучей в капле воды: а - при одном отражении, б - при двух отражениях. |
Из рис. 2, а видно, что падающий луч с одним отражением может быть воспринят наблюдателем, если только точка падения относится к верхней части капли (y > 0). Наоборот, при двух отражениях это окажется возможным для тех лучей, которые падают на нижнюю часть капли (y < 0).
Предположим сначала, что капля находится в вертикальной плоскости, проходящей через положение Солнца и глаз наблюдателя. Тогда падающий, преломленные и отраженные лучи лежат в этой же плоскости. Если α1 - угол падения, а α2 - угол преломления, то из рис. 2, а и б угол вышедшего луча по отношению к падающему в первом случае будет равен φ1= 4α2 -2α1 (1)
а во втором - φ2= π - 6α2 + 2α1 (2)
причем, согласно закону преломления: sin α2= sin α1/n
где n в нашем случае показатель преломления воды. Кроме того, принимая условно радиус капли за единицу длины, имеем:
|
sin α1= y |
sin α2= y/n |
φ1=4 arcsin(y/n) - 2 arcsin y, y>0 (3)
φ2= π+6 arcsin(y/n) - 2 arcsin y, y<0 (4)
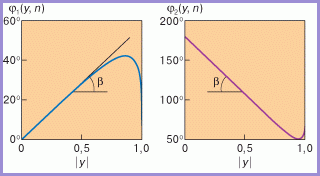
Эти два уравнения являются основными для дальнейшего рассмотрения. Нетрудно построить графики углов φ1 и φ2 как функций y. Они представлены на рис. 3 для показателя преломления n=1,331 (красный цвет). Мы видим, что при значении прицельного параметра y≈0,85 достигается максимум угла φ1, приблизительно равный 42°, а угол имеет минимум ~53° при y≈-0,95. Покажем, что этим экстремальным точкам соответствует максимум интенсивности отраженного каплей света.
|
|
|
Рис. 3. Зависимость угла отражения луча, падающего на каплю, от прицельного параметра. |
Рассмотрим некоторый малый интервал изменения прицельного параметра (для определенности в первом случае) y, y + Δy. С помощью графика можно найти изменение угла φ на этом интервале Δφ. На рис. 3 видно, что Δφ=Δy*tg β, где β - угол, который касательная к графику в данной точке образует с осью абсцисс. Величина Δy пропорциональна интенсивности света ΔI, падающего на каплю в этом интервале прицельного параметра. Эта же интенсивность света (точнее, пропорциональная ей величина) рассеивается каплей в угловом интервале Δφ. Мы можем написать ΔI ~ Δy =Δy*ctg β. Следовательно, интенсивность рассеянного каплей света, приходящаяся на единицу угла рассеяния, может быть выражена как I(φ) = ΔI/Δφ ~ ctg β (5)
Так как в экстремальных точках ctg β = ∞, то величина (5) обращается в бесконечность. Отметим, что положения этих экстремальных точек для различных цветов несколько отличаются, что и позволяет наблюдать радугу.
Как нарисовать радугу
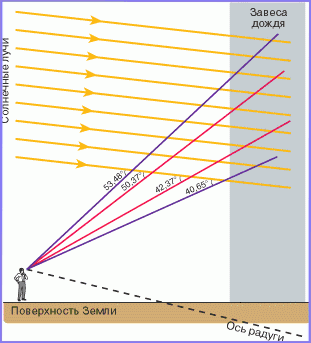
Теперь мы можем нарисовать схему наблюдения радуги. Такое построение выполнено на рис. 4. Сначала рисуем поверхность Земли и стоящего на ней наблюдателя. Перед наблюдателем находится завеса дождя (закрашенная серым цветом). Затем изображаем солнечные лучи, направление которых зависит от высоты Солнца над горизонтом. Через глаз наблюдателя проводим красные и фиолетовые лучи под указанными выше углами по отношению к солнечным лучам. Можно быть уверенным на основании результатов предыдущего раздела, что эти лучи возникнут в результате рассеяния на соответствующих каплях дождя. При этом, как следует из рис. 2, нижняя радуга обусловлена процессами рассеяния с одним отражением, а верхняя - с двумя отражениями. Обратите внимание на чередование цветов: фиолетовые лучи являются внешними, а красные - внутренними. Очевидно, что лучи других цветов в каждой радуге размещаются между красным и фиолетовым в соответствии со значениями показателей преломления.
|
|
|
Рис. 4. Схема наблюдения радуги. |
Напомним, что мы пока рассматривали изображение радуги в вертикальной плоскости, проходящей через глаз наблюдателя и положение Солнца. Проведем прямую, проходящую через глаз наблюдателя параллельно солнечному лучу. Если вертикальную плоскость поворачивать вокруг указанной прямой, то ее новое положение для наблюдения радуги будет совершенно эквивалентно исходному. Поэтому радуга имеет форму дуги окружности, центр которой находится на построенной оси. Радиус этой окружности (как видно на рис. 4) приблизительно равен расстоянию наблюдателя до завесы дождя.
Отметим, что при наблюдении радуги Солнце не должно стоять слишком высоко над горизонтом - не более чем на 53,48°. Иначе картина лучей на рисунке будет поворачиваться по часовой стрелке, так что даже фиолетовый луч верхней радуги не сможет попасть в глаз наблюдателя, стоящего на Земле. Правда, это окажется возможным, если наблюдатель поднимется на некоторую высоту, например на самолете. Если наблюдатель поднимется достаточно высоко, то он сможет увидеть радугу и в форме полной окружности.
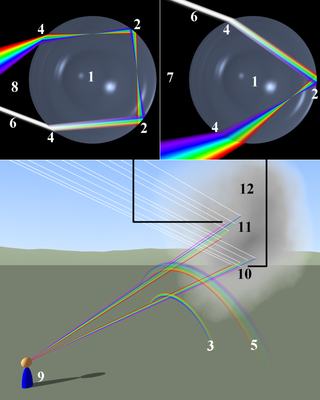
Схема образования радуги
Схема образования радуги
1) сферическая капля 2) внутреннее отражение 3) первичная радуга
4) преломление 5) вторичная радуга 6) входящий луч света
7) ход лучей при формировании первичной радуги
8) ход лучей при формировании вторичной радуги
9) наблюдатель 10) область формирования первичной радуги
11) область формирования вторичной радуги 12) облако капелек
Данное описание радуги следует уточнить c учетом того, что солнечные лучи не строго параллельны. Это связано с тем, что лучи, падающие на каплю от разных точек Солнца, имеют несколько различные направления. Максимальное угловое расхождение лучей определяется угловым диаметром Солнца, как известно равным приблизительно 0,5°. К чему это приводит? Каждая капля испускает в глаз наблюдателя не столь монохроматический свет, как это было бы в случае строгой параллельности падающих лучей. Если бы угловой диаметр Солнца заметно превосходил угловое расстояние между фиолетовым и красным лучами, то цвета радуги были бы неразличимы. К счастью, это не так, хотя, несомненно, перекрывание лучей с разными длинами волн влияет на контрастность цветов радуги. Интересно, что конечность углового диаметра Солнца была уже учтена в работе Декарта.